この記事では、Pythonで重回帰分析を簡単に行う方法を説明しています。
そのため、「重回帰分析とは?」という小難しいことは書いていません。
「とりあえず、Pythonで重回帰分析を試したい」人向けの記事内容です。
そして、そのための環境構築やプログラムについて説明しています。
あとは、標準化についても理解できるようになります。
実際の数値とともに説明しており、イメージしやすいと思います。
本記事の内容
- Pythonで重回帰分析を行うための環境
- とりあえず、Pythonで重回帰分析を行う
- 重回帰分析の精度(回帰係数・決定係数)
- Pythonで線形回帰の重回帰分析を行う方法【機会学習】のまとめ
まずは、今回の記事で利用している環境の説明からです。
Pythonで重回帰分析を行うための環境
- Windows 10 Home (バージョン1909)※以下の説明は64bit前提
- Python 3.7.3
- NumPy 1.18.5
- Pandas 0.24.2
- Matplotlib 3.2.1
- scikit-learn 0.20.3
Pythonの上記ライブラリは、すべてインストールしておいてください。
インストールコマンドを載せておきます。
pip install numpy pip install matplotlib pip install pandas pip install scikit-learn
Matplotlibのグラフを日本語化対応していない場合は、以下の記事をご覧ください。
この記事を参考にすれば、日本語化対応が簡単にできます。
とりあえず、Pythonで重回帰分析を行う
折角なので、実際のデータで分析してみます。
以下のページで表示されているデータを利用します。
https://senkyo-local.info/m_ranking/
https://senkyo-local.info/f_ranking/
議員報酬が、次の項目により予測できるかどうか?
- 都道府県
- 財政力指数
- 歳入
- 人口
- 面積
- 人口密度
この場合、議員報酬が目的変数です。
そして、上記の項目が説明変数となります。
データを準備する
なお、上記で示した選挙サイトは私が開発したモノです。
そのため、スクレイピングをせず、データベースよりデータを取得しています。
815市区のデータをcity_info.csvに保存します。
city_info.csvの内容(最初の5行)は、以下。

モジュール読み込み
とりあえず、重回帰分析を行います。
そのために必要なモジュールをimportします。
import numpy as np import pandas as pd from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression
データ読み込み
DataFrame (データフレーム)として、読み込みます。
# csv読み込み
df = pd.read_csv('./data/city_info.csv')
目的変数と説明変数を用意する
データフレームから抽出しています。
# 目的変数(Y) Y = np.array(df['annual_income']) # 説明変数(X) col_name = ['prefecture_id', 'population', 'area', 'population_density', 'fiscal_index', 'revenue'] X = np.array(df[col_name])
訓練(学習)データとテストデータを用意する
train_test_splitにより、簡単に分割しています。
# データの分割(訓練データとテストデータ) X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=0)
test_size=0.3にして、各データを次の比率に分割です。
訓練データ:テストデータ = 7:3
分割時点での各変数の状態は、以下。
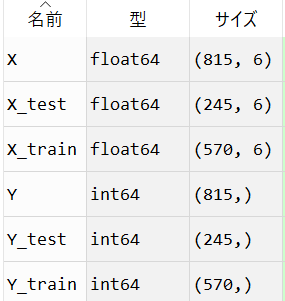
重回帰分析を実行する
これだけで重回帰分析ができるなんて、便利ですよね。
ライブラリの作成者に感謝です。
# モデル構築 model = LinearRegression() # 学習 model.fit(X_train, Y_train)
分析結果を確認する
結果を確認するコードは、以下。
# 回帰係数
coef = pd.DataFrame({"col_name":np.array(col_name),"coefficient":model.coef_}).sort_values(by='coefficient')
# 結果
print("【回帰係数】", coef)
print("【切片】:", model.intercept_)
print("【決定係数(訓練)】:", model.score(X_train, Y_train))
print("【決定係数(テスト)】:", model.score(X_test, Y_test))
とりあえず、ここまでのコードをすべて載せておきます。
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
# csv読み込み
df = pd.read_csv('./data/city_info.csv')
# 目的変数(Y)
Y = np.array(df['annual_income'])
# 説明変数(X)
col_name = ['prefecture_id', 'population', 'area', 'population_density', 'fiscal_index', 'revenue']
X = np.array(df[col_name])
# データの分割(訓練データとテストデータ)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=0)
# モデル構築
model = LinearRegression()
# 学習
model.fit(X_train, Y_train)
# 予測
#Y_pred = model.predict(X_test)
# 検証
#print(Y_test[:5])
#print(Y_pred[:5])
# 回帰係数
coef = pd.DataFrame({"col_name":np.array(col_name),"coefficient":model.coef_}).sort_values(by='coefficient')
# 結果
print("【回帰係数】", coef)
print("【切片】:", model.intercept_)
print("【決定係数(訓練)】:", model.score(X_train, Y_train))
print("【決定係数(テスト)】:", model.score(X_test, Y_test))
このコードの実行結果は、以下。
【回帰係数】 col_name coefficient 5 revenue -6.946525e-03 1 population 7.678455e+00 3 population_density 1.792167e+02 2 area 1.116185e+03 0 prefecture_id 1.211776e+04 4 fiscal_index 2.778381e+06 【切片】: 3657613.4779733205 【決定係数(訓練)】: 0.7270440949040748 【決定係数(テスト)】: 0.7148728383097965
とりあえず、Pythonで重回帰分析ができました。
あくまで、スタートに立っただけですけどね。
でも、これだけのコードで重回帰分析ができることを確認できました。
次以降は、上記の分析の結果について触れていきます。
そのため、「重回帰分析とは?」という小難しい話に入ってしまいます。
興味のある方は、引き続きご覧ください。
重回帰分析の精度(回帰係数・決定係数)
重回帰分析の結果において、ポイントになるのは以下。
- 回帰係数
- 決定係数
分析結果をもとにして、これらの係数について解説していきます。
回帰係数
回帰係数は、目的変数への影響度を表しています。
その影響度により、どの説明変数が目的係数に影響を与えたかを判別します。
分析の結果は、以下です。
| col_name | coefficient | |
| 5 | revenue | -0.006946524906 |
| 1 | population | 7.678455288 |
| 3 | population_density | 179.2167402 |
| 2 | area | 1116.185493 |
| 0 | prefecture_id | 12117.76435 |
| 4 | fiscal_index | 2778381.231 |
これは、明らかに桁が違いますね。
この回帰係数のことを、偏回帰係数と言います。
それぞれの変数を標準化(※)していないのです。
だから、桁が異なる値になってしまっています。
このままでは、使い物になりません。
尺度が違うと表現すればよいかもしれません。
(※)標準化
標準化とは、「各生データの平均値との差」を標準偏差で割ったものです、
かなり大雑把に言うと、比率にして単位を揃えるようなイメージになります。
変数を標準化する
標準化について、論より証拠で実際のデータで確認しましょう。
標準化する前の説明変数(X):最初の5行
| 1 | 1.96E+06 | 1121.26 | 1743.98 | 0.73 | 9.87E+08 |
| 1 | 258948 | 677.87 | 382 | 0.47 | 1.33E+08 |
| 1 | 116516 | 243.83 | 477.86 | 0.44 | 5.57E+07 |
| 1 | 337392 | 747.66 | 451.26 | 0.53 | 1.56E+08 |
| 1 | 84405 | 81.01 | 1041.91 | 0.62 | 4.30E+07 |
標準化した後の説明変数(X):最初の5行
| -1.58519 | 7.01458 | 3.00897 | -0.0450783 | 0.36448 | 7.158 |
| -1.58519 | 0.448712 | 1.44859 | -0.435846 | -0.702425 | 0.535835 |
| -1.58519 | -0.102531 | -0.0788783 | -0.408343 | -0.825529 | -0.0642061 |
| -1.58519 | 0.752308 | 1.6942 | -0.415975 | -0.456216 | 0.715903 |
| -1.58519 | -0.226808 | -0.651874 | -0.24651 | -0.0869031 | -0.163052 |
比較すれば、標準化の意味がわかりますね。
この標準化した変数を用いて、再び重回帰分析を行います。
標準化のために追加したのは、以下のコードです。
後で、また全コードを載せます。
from sklearn.preprocessing import StandardScaler ~ # 標準化 scaler = StandardScaler() scaler.fit(np.array(df)) df_std = scaler.transform(np.array(df)) df_std = pd.DataFrame(df_std,columns=df.columns)
変数を標準化した分析結果(回帰係数)は、以下。
| col_name | coefficient | |
| 5 | revenue | -0.4354990372 |
| 0 | prefecture_id | 0.07687798468 |
| 2 | area | 0.1542165142 |
| 3 | population_density | 0.3037167989 |
| 4 | fiscal_index | 0.3292135998 |
| 1 | population | 0.9646640639 |
この回帰係数のことを標準化偏回帰係数と言います。
これで使えるデータになりました。
population(人口)が、目的変数(議員報酬)に最も影響を与えるようです。
revenue(歳入)は、もっとも影響を与えないことになります。
本当にこの結果が正しいのかどうか、別の角度から検証したいですね。
また、別の記事でやってみようと思います。
決定係数
決定係数は、その回帰分析の精度を表す指標です。
分析結果の決定係数(訓練)は、0.7270440949040748です。
適当に分析した割には、そこそこ精度の高い数値です。
目安としては、0.5以上のようです。
目標は、0.8という記述が多いですね。
その意味では、大した調整もせずに0.72以上はいい感じです。
幸先いい分析のスタートと言えるでしょう。
Pythonで線形回帰の重回帰分析を行う方法【機会学習】のまとめ
まず、完成したコードを載せておきます。
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
# csv読み込み
df = pd.read_csv('./data/city_info.csv')
# 標準化
scaler = StandardScaler()
scaler.fit(np.array(df))
df_std = scaler.transform(np.array(df))
df_std = pd.DataFrame(df_std,columns=df.columns)
# 目的変数(Y)
Y = np.array(df_std['annual_income'])
# 説明変数(X)
col_name = ['prefecture_id', 'population', 'area', 'population_density', 'fiscal_index', 'revenue']
X = np.array(df_std[col_name])
# データの分割(訓練データとテストデータ)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=0)
# モデル構築
model = LinearRegression()
# 学習
model.fit(X_train, Y_train)
# 回帰係数
coef = pd.DataFrame({"col_name":np.array(col_name),"coefficient":model.coef_}).sort_values(by='coefficient')
# 結果
print("【回帰係数】", coef)
print("【切片】:", model.intercept_)
print("【決定係数(訓練)】:", model.score(X_train, Y_train))
print("【決定係数(テスト)】:", model.score(X_test, Y_test))
Pythonで簡単に重回帰分析を行う方法を説明してきました。
実は、これは機械学習の説明でもあります。
もっと言うと、教師あり学習の機械学習です。
機械学習と聞くと構えてしまいませんか?
私は、どうしても構えてしまいますね。
だから、この記事で機械学習というワードをここまで使いませんでした。
機械学習というより、より精度の高い線形回帰の分析を行うことが目的でした。
それが重回帰分析でした。
そして、その重回帰分析は、機械学習だったということです。
このような感じで分析について進めていけば、ディープラーニングにも到達できるかもしれません。