共起ネットワークに関して調べていますか?
そうであれば、「Jaccard係数」を何度か目にしていませんか?
その際に、「うわっ~、集合とか数学かよ・・・」
このように思った方に、朗報です。
数学と言っても、そんなに大したことはありません。
Jaccard係数では、機械学習のようにわけのわからない数式は出てきません。
むしろ、簡単なロジックでJaccard係数の実装が可能です。
そして、そうすることはPythonの勉強にもなります。
そのため、Jaccard係数を学ぶことは一石二鳥と言えます。
本記事の内容
- Jaccard係数とは?
- Jaccard係数をPythonで計算する
それでは、上記に沿って解説していきます。
Jaccard係数とは?
Jaccard(ジャッカード)係数とは、二つの集合がどのくらい似ているのか表す指標です。
ちょっと難しく言うと、集合の類似度を測る指標となります。
集合の類似度に関して、「Python」と「機械学習」を用いて考えてみます。
次の2つの文を見てください。
Pythonは、機械学習でよく利用されるプログラム言語である。
Pythonは、機械学習だけではなく、Webアプリ開発などでも利用されている。
両方の文で、「Python」と「機械学習」が含まれています。
このとき、「Python」と「機械学習」が「共起」していると言えます。
この「共起」をもとすれば、Jaccard係数を求めることができます。
例えば、以下の条件の文があったとします。
- 「Python」を含む文が180個
- 「機械学習」を含む文が40個
- 「Python」と「機械学習」の両方を含む文が20個
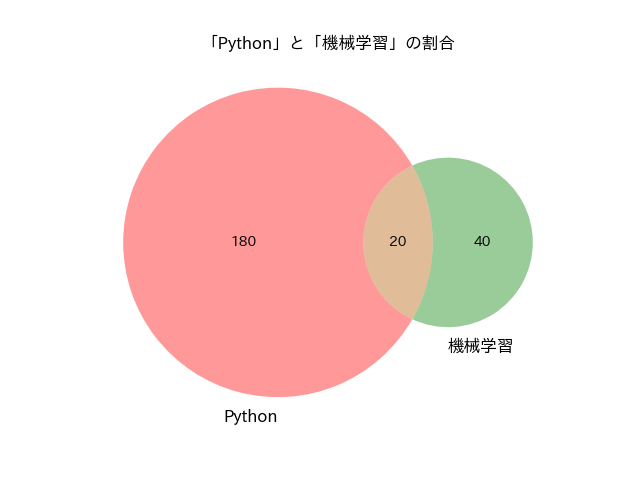
「Python」の集合をA、「機械学習」の集合をBとします。
この場合、Jaccard係数[J(A,B)]は以下のように計算できます。
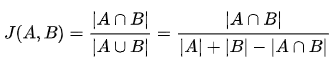
この計算式に値を入力していきましょう。
20 ÷ (180 + 40 – 20) = 20 ÷ 200 = 0.1
よって、Jaccard係数は0.1となります。
Jaccard係数が大きいほど、「Python」と「機械学習」は近い(類似している)と判断されます。
今回の例では、「Python」と「機械学習」が近いとは決して言えません。
以上、Jaccard係数に関する説明でした。
次では、実際にPythonでJaccard係数を計算していきます。
ちなみに、上記で用いたベン図はPythonで作成しています。
Jaccard係数をPythonで計算する
Pythonでは、標準で集合を扱うことが可能です。
具体的には、setオブジェクトを用います。
まずは、A集合とB集合を用意します。
# 初期化
A = set()
B = set()
# A集合に180個の要素追加(0~179)
for i in range(180):
A.add(i)
# B集合に40個の要素追加(160~199)
for i in range(40):
B.add(i+160)
次に、積集合「A ∩ B」を求めます。
# 積集合「A ∩ B」 AB_intersection = A.intersection(B)
関数一つで積集合を求めることができます。
AB_intersectionは、160~179の値となっています。
ここまで求まれば、Jaccard係数を計算できます。
# Jaccard係数 jaccard = len(AB_intersection) / (len(A) + len(B) - len(AB_intersection)) print(jaccard)
上記のプログラムを実行した結果は、「0.1」が表示されます。
「Jaccard係数とは?」で表示した値と同じですね。
どうでしたか?
何も難しい計算式は出来てきませんでした。
関数化しておけばいろいろと使えそうですね。
そうは言っても、Jaccard係数を求めるのがゴールではありません。
Jaccard係数はあくまで、集合同士の類似を判断するために利用する指標です。
テキストマイニングの分野なら、単語間の類似性(距離)を導き出します。
そして、それらの情報をもとに共起ネットワークを作成することになります。
本ブログでは、共起ネットワークについて扱っていく予定です。
その際には、今回のJaccard係数が大活躍します。