ダイクストラ法をPythonで実行する方法を解説します。
ただし、ダイクストラ法のアルゴリズムを実装などしません。
実装などせず、ライブラリに依存します。
「車輪の再発明」ほど時間の無駄になることはありません。
本記事の内容
- NetworkXライブラリでダイクストラ法が実行可能
- ダイクストラ法に関する関数一覧
- ダイクストラ法の練習問題をPythonで解く
それでは上記に沿って解説していきます。
NetworkXライブラリでダイクストラ法が実行可能
本記事では、「ダイクストラ法(Dijkstra’s algorithm)とは?」については扱いません。
ダイクストラ法については、多くのサイトで詳しく説明してくれています。
そのため、Pythonでダイクストラ法を実行する方法に絞って解説していきます。
そして、実装するのではなくライブラリに依存する形での実行方法を解説します。
では、そのための前提となるライブラリを紹介しましょう。
そのライブラリとは、ネットワーク分析を行うためのNetworkXです。
NetworkXに関しては、次の記事で解説しています。
インストールから、簡単な使い方までまとめています。
よって、以下で説明するプログラムには、NetworkXのインストールが必須です。
そのため、上記記事でNetworkXのインストールまで完了させてください。
次では、NetworkXで用意されているダイクストラ法に関する関数を確認します。
ダイクストラ法に関する関数一覧
NetworkX公式 最短経路に関する関数一覧
https://networkx.org/documentation/stable/reference/algorithms/shortest_paths.html
全部で以下の13個が確認できました。
- dijkstra_predecessor_and_distance(G, source)
- dijkstra_path(G, source, target[, weight])
- dijkstra_path_length(G, source, target[, weight])
- single_source_dijkstra(G, source[, target, …])
- single_source_dijkstra_path(G, source[, …])
- single_source_dijkstra_path_length(G, source)
- multi_source_dijkstra(G, sources[, target, …])
- multi_source_dijkstra_path(G, sources[, …])
- multi_source_dijkstra_path_length(G, sources)
- all_pairs_dijkstra(G[, cutoff, weight])
- all_pairs_dijkstra_path(G[, cutoff, weight])
- all_pairs_dijkstra_path_length(G[, cutoff, …])
- bidirectional_dijkstra(G, source, target[, …])
今回は、このうちの5個を利用します。
なお、引数に関しては以下を参考にしてください。
| G | グラフデータ |
| source | 開始ノード |
| target | 終了ノード |
| weight | ノード間の重み |
今は、「ふーん」レベルでOKです。
実際に利用しているコード部分を見れば、理解できるはずです。
ダイクストラ法の練習問題をPythonで解く
東京大学大学院での行われた離散数学に関する講義内容のPDF
https://www.hongo.wide.ad.jp/~jo2lxq/dm/lecture/08.pdf
上記PDFの8ページを見てください。
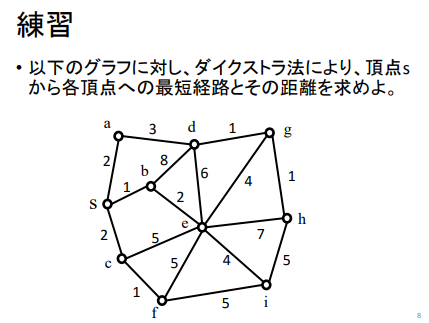
この練習問題をPythonで解いていきましょう。
上記問題のノード関係(重み含む)を以下のテキストにまとめました。
data.txt
a s 2 a d 3 b s 1 b d 8 b e 2 c s 2 c e 5 c f 1 d e 6 d g 1 e f 5 e i 4 e g 4 f i 5 g h 1 h i 5
正直、これを用意するのが一番面倒かもしれません。
このdata.txtのデータを利用して、最短経路問題をダイクストラ方法で解いていきます。
dijkstra_path系
習うより慣れろです。
import networkx as nx
# ファイルの読み込み
G = nx.read_weighted_edgelist('data.txt')
path = nx.dijkstra_path(G, "s", "a")
length = nx.dijkstra_path_length(G, "s", "a")
print(path)
print(length)
上記コードを実行した結果は、以下。
['s', 'a'] 2.0
「dijkstra_path(G, “s”, “a”)」は、頂点sと頂点aへの最短経路をリスト型で返します。
「dijkstra_path_length(G, “s”, “a”)」は、頂点sと頂点aへの距離(重み)を返します。
ただ、練習問題では頂点sから各頂点への最短経路と距離を求めています。
dijkstra_path(G, “s”, “b”)、dijkstra_path(G, “s”, “c”)、・・・
dijkstra_path_length(G, “s”, “b”)、dijkstra_path_length(G, “s”, “c”)、・・・
上記のように地道にやっていけば問題は解けるでしょう。
でも、面倒過ぎます。
そこで次の関数が用意されています。
single_source_dijkstra系
import networkx as nx
# ファイルの読み込み
G = nx.read_weighted_edgelist('data.txt')
path = nx.single_source_dijkstra_path(G, "s")
length = nx.single_source_dijkstra_path_length(G, "s")
print(path)
print(length)
上記コードを実行した結果は、以下。
{'s': ['s'], 'a': ['s', 'a'], 'b': ['s', 'b'], 'c': ['s', 'c'], 'd': ['s', 'a', 'd'], 'e': ['s', 'b', 'e'], 'f': ['s', 'c', 'f'], 'i': ['s', 'b', 'e', 'i'], 'g': ['s', 'a', 'd', 'g'], 'h': ['s', 'a', 'd', 'g', 'h']}
{'s': 0, 'b': 1.0, 'a': 2.0, 'c': 2.0, 'e': 3.0, 'f': 3.0, 'd': 5.0, 'g': 6.0, 'i': 7.0, 'h': 7.0}
「single_source_dijkstra_path(G, “s”)」は、頂点sから各頂点への最短距離を辞書型で返します。
「single_source_dijkstra_path_length(G, “s”)」は、頂点sから各頂点への最短(重み)を辞書型で返します。
なお、上記の関数の処理を一度に行うのが以下の関数です。
length, path = nx.single_source_dijkstra(G, "s")
まとめ
以下が解答です。
PDFの9ページ目に載っています。
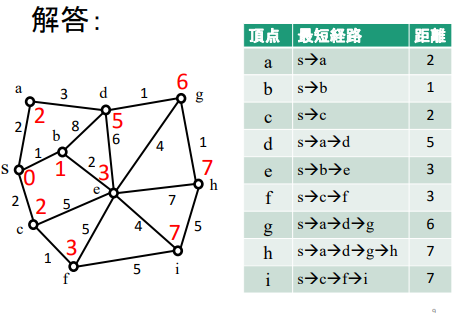
一つだけ誤記があります。
解答の方にです。
頂点sと頂点iの最短経路を見てください。
s→c→f→iとなっています。
しかし、この経路の距離は8となります。
正解は、[‘s’, ‘b’, ‘e’, ‘i’]です。
これだと距離は7になります。
おそらく、講義では修正があったとは思います。
でも、これは人間がやるからこそのミスです。
プログラムでできるモノなら、すべてプログラムにやらせればいいのです。
そして、そのプログラムも自分で実装するよりは、ライブラリなどに頼ればいいのです。
そうすれば、ミスもなくなります。
それに処理速度もライブラリなら、自分で実装したものよりも高速のはずです。