フーリエ変換というワードを知っていますか?
機械学習を触るようになると、ちょこちょこ目にします。
フーリエ変換は、計算方法(アルゴリズム)です。
数学的に理解するには、非常に難しいようです。
ただ、個人的には計算式に興味はありません。
あくまで、ツール(考え方)として使えるかどうかに興味があります。
その意味では、知っておけばどこかで使えそうな考え方です。
そのためにも、まずは実践して記憶に残します。
本記事の内容
- Pythonで高速フーリエ変換を行うには?
- Numpyのインストール
- NumpyでFFTの実行
FFTは、fast Fourier transformの略称です。
日本語で、高速フーリエ変換となります。
それでは、上記に沿って解説していきます。
Pythonで高速フーリエ変換を行うには?
「フーリエ変換とは?」などは、説明しません。
わかりやすく説明している記事が、Googleで多く見つけることができます。
是非、それらの記事で理解してください。
この記事では、Pythonで高速フーリエ変換を行う方法を解説することに専念します。
このような場合、Pythonは有利ですよね。
高度な計算を行うためのライブラリが多く存在しています。
パッと思いつくだけも、以下があります。
- Numpy
- Matplotlib
- Scipy
Pythonを触っていれば、どれも見たことがあるようなモノばかりです。
今回は、Numpyを用いて高速フーリエ変換を試していきます。
そのためには、まずはNumpyのインストールですね。
Numpyのインストール
Numpyの最新バージョンは、1.19.5となります。
この最新バージョンは、2021年1月6日にリリースされています。
サポートOSに関しては、以下を含むクロスプラットフォーム対応です。
- Windows
- macOS
- Linux(Ubuntu、Debianなど)
サポート対象のPythonのバージョンは、3系です。
Python 3系ならどのバージョンでも問題はありません。
ちなみに、インストールしていく環境は以下のバージョンです。
>python -V Python 3.9.1
2021年1月時点では、最新版のPythonとなります。
では、Numpyをインストールします。
最初に、現状のインストール済みパッケージを確認しておきます。
>pip list Package Version ---------- ------- pip 20.3.3 setuptools 51.3.3
次にするべきことは、pip自体の更新です。
pipコマンドを使う場合、常に以下のコマンドを実行しておきましょう。
python -m pip install --upgrade pip
では、Numpyのインストールです。
Numpyのインストールは、以下のコマンドとなります。
pip install numpy
インストールは、一瞬で終わります。
では、どんなパッケージがインストールされたのかを確認しましょう。
>pip list Package Version ---------- ------- numpy 1.19.5 pip 20.3.3 setuptools 51.3.3
Numpyの最新版が、インストールされています。
Numpyは、依存ライブラリがありません。
次は、NumpyでFFTの実行を行いましょう。
NumpyでFFTの実行
NumpyだけでFFTを実行できます。
しかし、それをグラフにしないと意味がわかりません。
そのため、グラフを表示するためにMatplotlibを利用します。
もしインストールしていない場合は、インストールしておいてください。
以下のpipコマンドを実行するだけです。
pip install matplotlib
Matplotlibのインストールは、簡単です。
しかし、日本語化が若干面倒です。
もしまだ、Matplotlibを日本語化していないなら次の記事を参考にしてください。
準備が整ったら、次のコードを実行します。
import numpy as np
import matplotlib.pyplot as plt
# データのパラメータ
N = 90 # サンプル数
dt = 0.01 # サンプリング間隔
f1, f2 = 10, 40 # 周波数
t = np.arange(0, N*dt, dt) # 時間軸
freq = np.linspace(0, 1.0/dt, N) # 周波数軸
# 信号を生成(周波数f1の正弦波+周波数f2の正弦波)
signal = np.sin(2*np.pi*f1*t) + np.sin(2*np.pi*f2*t)
# グラフ表示
fig = plt.figure(figsize=(12, 5))
# 左の図
ax1 = fig.add_subplot(121)
plt.plot(t, signal)
plt.xlabel("秒 [s]", fontsize=15)
plt.ylabel("シグナル", fontsize=15)
# 高速フーリエ変換(FFT)
F = np.fft.fft(signal)
# 振幅スペクトルを計算
amplitude = np.abs(F)
# 調整
F_amplitude = amplitude / N * 2
F_amplitude[0] = F_amplitude[0] / 2
# 右の図
ax2 = fig.add_subplot(122)
plt.plot(freq[:int(N/2)+1], F_amplitude[:int(N/2)+1])
plt.xlabel("周波数 [Hz]", fontsize=15)
plt.ylabel("振幅スペクトル", fontsize=15)
# 画像保存
plt.savefig("test.png")
上記のプログラムを実行すると、次の画像が作成されます。
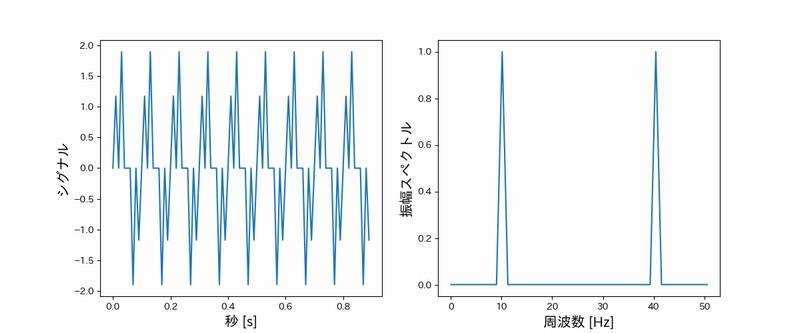
高速フーリエ変換の説明でよく出てくるグラフです。
プログラムの内容を簡単に説明します。
周波数10Hz、40Hzを持つ信号(signal)を用意します。
普通は、音声ファイルなどを読み込んで取得することになります。
この信号を時系列で表示したのが左のグラフです。
右の図は、周波数毎の成分の構成を現したグラフです。
用意した信号には、ノイズが一切ありません。
そのため、10Hzと40Hzしか周波数が存在していません。
時系列で表現されたグラフから、その要素(周波数)の構成比率が判明します。
こんなことができるのが、高速フーリエ変換です。
フーリエ変換を説明する際には、いろいろと難しい表現があります。
ただ、個人的にはこれぐらいザックリとした理解です。
もちろん、これはフーリエ変換のごく一部であることは理解しています。
以上、NumpyでFFTを実行する方法について、実際のコードで説明しました。



